Оддсы и ауты – математика в покере

Если вы хотите играть в покер успешно, вы не можете обойтись без математики и вычисления вероятностей. Много людей пытаются пропустить это, допуская каждый раз одни и те же ошибки. Давайте посмотрим, что такое оддсы и аутсы и как легкая математика в покере может повлиять принять правильное решение.

Научите здесь основные турнирные стратегии Харрингтона!

Оддсы это вероятность выиграть руку. Например рука АА выиграет руку 88 в 80% случаев. Ауты называются карты, которые могут превратить данную руку в успешную. Возьмем следующий пример: у вас на флопе есть Q95 rainbow, а ваша начальная рука Jto. Если тут у вашего оппонента есть QQ, то нам поможет один из восьми аутов сделать стрейт. В этом случае вам нужно один из четырех оставшихся королей или восьмерок.

Давайте представим себе, что пот на этом флопе 100 фишек, а ваш соперник делает олл-ин с его оставшимися 50 фишками. Сделать ли нам колл или нет? В подобной ситуации есть одно золотое правило – определить вероятность выиграть в зависимости от аутов: так называемое 2-4 правило. Нужно определить число аутов и умножить на 4 на флопе, а на терне на 2 и так получите приблизительную вероятность попасть во время игры на один из аутов. Этот способ очень легкий для применения, так что вам даже не надо пользоваться калькулятором. Если загрузите бесплатную специальную программу для вычисления вероятностей PokerStrategy Equilator, можете увидеть точные результаты. Но применяя правило 2-4 без помощью калькулятора стоимости выходят очень близкими с теми же из программы.

Покер математика – пот-оддсы

После того как мы узнаем приблизительную вероятность выиграть, нам надо сравнить ее с соотношением величины пота к величине колла – так называемые пот-оддсы. Давайте посмотрим следующие примеры:

• 9 аутов на флопе (напр. Flush Draw) – около 36,9% (~1/2)
• 2 аута на терне (сет на ривере) – около 4,5% (~1/20)

На столе есть 150 фишек, а данный колл стоит вам 50 фишек – это и есть 1:3. Если вероятность победить хороша, вам рекомендуется сделать колл, если нет – лучше сделать фолд. Если мы сделаем Flush Draw, мы выиграем один из трех шоудаунов, что соответствует оддсам ½ и колл здесь абсолютно правильное решение.
Ко второму примеру наши оддсы прибыли составляют 1/20 и нам вполне ясно, что надо сделать фолд. В зависимости от математического ожидания (Expected Value) мы ясно понимаем все последствия колла без соответных пот-оддсов (pot odds) и вероятности выиграть.

Вычисление математического ожидания (Expected Value)

Вы можете все понять с так называемый математическим ожиданием. Если у вас есть Flush Draw вероятность выиграть 150 фишек 36,9%, но в остальных 63,1% мы потеряем 50 фишек.
Это простая покер математика показывает нам, что можем выиграть 23,8 фишек. Всегда имейте в виду, что сумма всех плохих и хороших решений в покере определяет вашу общую прибыль в покерной карьере.

А сейчас давайте сделаем вычисления для нашего примера с двумя аутсами, если допустим, что вы делаете те же самые ставки на терне:
Здесь видно, что колл в любом случае невыгоден и нам надо сразу же сделать фолд. Если математические ожидания отрицательны, будет бесмыслено продолжать играть. Когда накопите больше опыта в покере, будете хорошо оценивать у каких из многих опций есть самое большое математическое ожидание, чтобы увеличить прибыль. Но как начало, вам нужно научиться избежать больших ошибок, а именно предпринимать невыгодные коллы.

Покер математика – предполагаемые оддсы (Implied Odds)

Давайте немножко изменим пример с Flush Draw и сделаем его более интересным. Допустим, что у нас Nut Flush Draw на терне и с 9 аутами вероятность у нас выиграть около 18%. В поте опять есть 150 фишек, а колл будет нам стоит 50 фишек. Ни мы, ни оппонент сделали олл-ин и у нас есть достаточно фишек. Вопрос тут можем ли сделать колл? А ответ – нет. Наши шансы выиграть колл очень маленькие. Пока что все это правильно, но мы не увидели так называемых предполагаемых оддсов (Implied Odds) – на ривере можем выиграть еще больше фишек, если встретим флеш. Здесь ситуация немножко потруднее, так как мы не знаем сколько точно фишек можем взять от оппонента. Но за то можем вычислить сколько им как минимум надо быть, чтобы наш кол на терне был успешным.

В поте есть 150 фишек, а колл стоит 50. Шансы на прибыль около 18%. Если мы не встретим флеш, мы не будем инвестировать больше фишек в поте. Сейчас согласно шансам победить можем вычислить для какого пота был бы успешным колл величины 50 фишек. Это правило поможет вам в такой ситуации.
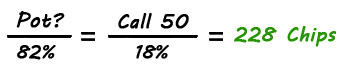Если в поте минимум 228 фишек, то кол с 50 фишками был бы выгодным. Но в нашем реальном поте есть 150 фишек, т.е. в поте должно быть на 78 фишек больше и именно эту сумму нам надо выиграть на ривере от соперника.

Implied Odds & Set Value – Poker math

Предполагаемые оддсы вычисляются очень просто. С их помощью можем узнать стоит ли нам сделать рейз перед флопом, если у нас средняя по силе покер пара. Давайте рассмотрим следующий пример: блайнды 25/50, UTG (under the gun, в нашем случае игрок в ранней позиции) обладает 5000 фишками, а мы сидим на баттоне и у нас 4000 фишек. UTG делает рейз 400 фишками (4 большие блайда) и мы думаем, что у игрока есть сильная пара. В конце концов все игроки делают фолд, после чего мы обнаруживаем, что у игрока была слабая покер пара из двух шестерoк. А сейчас давайте допустим, что на флопе появится сет, чтобы мы могли выиграть нашу руку дальше. Сделать ли нам колл, или нет? Давайте сначала увидим насколько большая вероятность сета на флопе. Это можем очень просто вычислить, если допустим, что вероятность появления сета на флопе нулевая. Тогда мы знаем только наши две карты, а остальные 50 совсем незнакомые для нас. К тому же здесь не имеет никакого значения сколько игроков получили скрытых карт и сколько на столе, все карты, пока что неизвестны для нас. Так вероятность, что первая флоп карта не одна из остальных шестерок 48/50, а для второй карты 46/49, так как мы знаем еще одну новую третью карту. Для третьей карты на флопе шансы уже 46/48. Вычисляя эти вероятности, мы получаем следующий результат:
Только в 12% из случаев мы встретим наш сет, но также нет и стопроцентного победителя в руке. Мы потеряем в игре против соперников с высокими сетами, стрейтами или флешами. А сейчас допустим, что у нас 10% вероятность выиграть. В этом случае если мы хотим ответить на рейз UTG игрока перед флопом, мы должны выиграть как минимум 10 раз больше чем колл. Это нужно, чтобы уравновесить ситуацию с другими 90% из случаев, в которых можете проиграть все ставки. Часто бывает, что с нашим сетом не получаем достаточно фишек от противника – например для руки QQ, он откажется, если в флопе AK9. Чтобы выравнить шансы нам надо сделать колл на Set Value, если на флопе можем как минимум 20 раз больше сделанного нами колла.
Давайте вернемся к первоначальному примеру. У UTG игрока есть после рейза в 200 фишек уже 4800, а мы после нашего колла 3800. Так как наш стек меньше, нам надо вычислить так называемый эффективный стек. 20 раз умножим на 200 фишек (наш колл), что делает 4000. В этом случае можем сделать колл. Он не был бы успешным, если эффективный стек у нас меньше. Если он например в 10 раз меньше, это делает 2000 фишек. В зоне между 10 и 20 разами прибыль зависит от умений и от того насколько сильно верите, что можете победить соперника, если бы не встретили сет.

Implied Odds для Drawing Hands – математика в покере

Если у вас drawing hands вам будет намного труднее выиграть на шоудауне, чем если у вас была покерная пара. Правило здесь говорит, что колл для коннекторов одной масти перед флопом стоит только тогда, когда можем выиграть в 25 раз больше его, а для коннекторов разной масти даже в 30 раз больше.
Вспомните об этом правиле, когда в первом блайнд уровне в SnG начинаете с 75 больших блайндов (10/20 для 1500 фишек). Колл, который в три раза выше большого блайнда, с коннекторами одной масти, трудно будет успешным, даже если рука с 89 одной масти выглядеть очень привлекательной.

Исключения из правил

Все эти правила в poker math могут в определенных ситуациях оказаться неправильными. Если играете против неопытных игроков, которые часто не могут сделать себе руку и оплачивают все ставки перед ривером, то у вас есть намного больше шансов победить. Тоже самое относится и к поту, где много игроков. Если появится сильная карта, а у вас спекулятивные руки, вполне вероятно найти игрока, у которого довольно сильная рука и который готов заплатить вам все.