Das Independent Chip Model (ICM)

Das ICM ist ein Modell, welches in Turnieren anhand der Anzahl eurer Chips den Erwartungswert für einen Turniergewinn errechnet. Hier erklären wir euch, wie diese Erwartungswerte eure Entscheidungen für ein All-In beeinflussen können. Alle Beispielrechnungen werden hier mit Hilfe des SnG Wizard vorgenommen. Dieses Programm ist das marktführende ICM Poker Tool und für einen kostenlosen Test als Free-Trial Version als Download erhältlich.

Die Wahrscheinlichkeit ein Turnier zu gewinnen

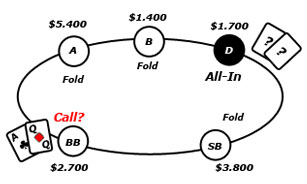
Das Independent Chip Model ist bei allen Arten von Turnieren anwendbar, anhand eines 10-Spieler Sit&Go mit Standard-Auszahlung lässt sich das Prinzip dieses Modells aber am besten veranschaulichen. Betrachten wir einmal die Situation an der Bubble. Hätten alle vier Spieler gleich große Chip Stacks, so hat jeder von ihnen die gleiche Chance auf dem ersten, zweiten, dritten oder vierten Platz abzuschließen. Wie sieht es aber mit unterschiedliche großen Stacks aus?

Spieler 1 steht mit 5800 recht gut da und hat nicht nur eine große Chance auf einen Platz in den Auszahlungen, sondern auch die besten Voraussetzungen für den Sieg. Spieler 2 dagegen hat mit seinen 1700 verbliebenen Chips die “allerbesten” Chancen als Bubble Boy das Turnier zu beenden. Spieler 3 und 4 haben ähnlich große Stacks und werden sich wahrscheinlich den zweiten und dritten Platz teilen. Natürlich kann jederzeit etwas Unvorhergesehenes passieren. Spieler 2 kann einen guten Lauf haben, mehrmals verdoppeln und letztendlich das Turnier gewinnen. Spieler 4 könnte ein All-In gegen Spieler 1 verlieren und ohne Auszahlung ausscheiden. Ja selbst Spieler 1 kann mit ein wenig Pech als Bubble Boy enden. Abhängig von den Stackgrößen ergeben sich folgende Wahrscheinlichkeiten für jede einzelne Platzierung:

Wahrscheinlichkeiten und Erwartungswerte der verschiedenen Stacks

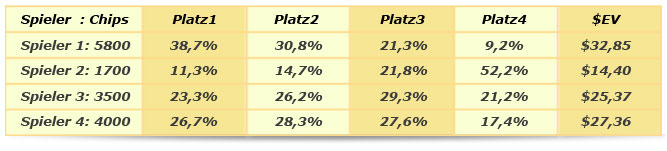Die Summe jeder Zeile und Spalte muss wieder 100% ergeben, die Spalte für den $EV ergibt zusammengerechnet den gesamten Preispool von $100. Anhand der Gewinnwahrscheinlichkeiten kann mit der Auszahlungsstruktur für jeden Spieler sein Erwartungswert für einen Geldgewinn berechnet werden – genannt $Expected Value($EV). In diesem Beispiel erhält bei einem BuyIn von $10 der erste Platz $50, Platz 2 $30 und Platz 3 $20.
Spieler 1 $EV = (38,7% x $50) + (30,8% x $30) + (21,3% x $20) + (9,2% x $0)

Spieler 1 $EV = $19,35 + $9,24 + $4,26 + 0 = $32,85

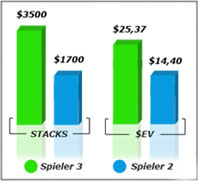Mit 5800 Chips besitzt Spieler 1  zur Zeit einen $EV von $32,85. Wenn wir diese Rechnung auch für die anderen Spieler durchführen, erhalten wir eine $EV von $14,40 für Spieler 2, $EV 25,37 für Spieler 3 und $EV 27,36 für Spieler 4 – insgesamt ergibt sich damit der Preispool von $100 (abgesehen von Rundungsfehlern).

Wenn wir uns diese Zahlen aber näher anschauen fällt auf, dass Spieler 3 mehr als doppelt so viele Chips besitzt wie Spieler 2. Sein $EV liegt aber unter dem Doppelten von Spieler 2. Warum das so ist und wie das Independent Chip Model unsere Entscheidungen bei All Ins beeinflusst, erfahrt ihr in den nächsten Abschnitten.

ICM Poker – Erwartungswerte und deren Konsequenzen

Warum ist die $EV von Spieler 3 nicht auch doppelt so hoch wie sein Chip Stack Spieler 2 gegenüber? Betrachten wir dazu zwei Extremsituationen: den Start und das Ende des Turniers. Am Anfang besitzen alle 1500 Chips und haben die gleiche Chance auf den Sieg des SnG´s. Die $EV für jeden Spieler beträgt wie das Buy In $10. Ist das Turnier vorüber, hat ein Spieler alle 15.000 Chips angehäuft, bekommt aber nur $50 des gesamten $100 Preispools als Gewinn ausgezahlt – seine Chips sind zu diesem Zeitpunkt nur noch die Hälfte wert. Was bedeutet dies nun für unsere ICM Poker Strategie?

Mit Hilfe des Independent Chip Model können wir nun herausfinden, wie sich in bestimmten Situationen unser $EV verändert. Wir spielen nun nicht mehr allein für Chips oder weil wir uns im Showdown vorn sehen – wir richten unsere Aktionen jetzt einzig und allein nach dem $EV. Selbst wenn dies bedeutet, dass wir vor dem Flop Asse folden müssten! Unglaublich? Dann lest weiter…

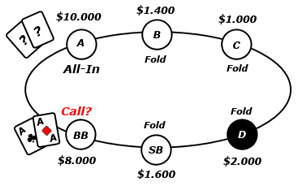Beispiel: Bubble eines Double or Nothing Sit&Go. Wir haben nach dem Chip Leader mit Abstand die meisten Chips und die restlichen 4 Spieler sind allesamt Short Stacks. Der Chip Leader geht All In, alle anderen folden und wir sitzen im Big Blind mit AA. Der Chip Leader hat diesen Move bereits in jeder der letzten fünf Hände gemacht und er könnte jede beliebige Hand halten – sollen wir callen? Dies ist natürlich ein extremes Beispiel, zeigt aber hervorragend wie das Independent Chip Model eure Entscheidungen beeinflusst. Durch die Stackgrößen der einzelnen Spieler und die DoN Auszahlungsstruktur(alle Gewinner erhalten das gleiche Preisgeld) befinden wir uns schon so gut wie im Geld – es muss nur noch einer der 4 Short Stacks das Spiel verlassen und das Turnier ist beendet. Unser $EV ist daher schon rechte nah am maximal möglichen Wert. Gegen seine Hand Range(any two) sind wir mit unseren Assen rund 85% Favorit, haben aber auch eine 15% Chance an der Bubble das Turnier ohne Auszahlung zu verlassen. Der Zugewinn von weiteren Chips hat nahezu keinen Mehrwert für uns, unsere $EV würde sich in 85% der Fälle nur minimal vergrößern. Allerdings haben wir eine 15% Chance unsere gesamte $EV zu verlieren – ein klarer Fold.

In Zahlen sieht dieses Beispiel so aus. Der Chip Leader besitzt 10.000 Chip, wir 8000, die vier Small Stacks jeweils zwischen 1000 und 2000. Durch die Auszahlungsstruktur eines DoN erhalten alle Gewinner für ihr $10 BuyIn $20 Preisgeld. Der Chip Leader besitzt mit seinen Chips rund $EV 19,94, wir $EV 19,89. Im Falle eines Turniergewinns würden wir den Wert auf $EV 20 vergrößern – das ist ein Plus von gerade einmal 0,11. Verlieren wir aber, sinkt unser $EV auf 0 – ein Minus von ganzen 19,89. Vergleichen wir dies mit unseren Gewinnchancen so erhalten wir (85% x 0,11) + (15% x -19,89) = 0,0935 +  (-2,9835) = -2,89. Ein Fold würde bedeuten, dass sich unser $EV nicht verändert.

In diesem Fall ist also der Fold die Aktion, die uns den höchsten Erwartungswert bietet und dies sollte eure einzige Entscheidungsgrundlage für ein All-In in einem Turnier darstellen.

Beispielrechnung einer alltäglichen ICM Poker Situation

Wir spielen ein reguläres SnG mit $10 BuyIn und Standard Auszahlungsstruktur. Insgesamt sind noch 5 Spieler verblieben, die folgenden Stackgrößen und $EV besitzen:

• Spieler 1: 5400 – $EV 30,54
• Spieler 2: 1400 – $EV 11,28
• Spieler 3: 1700 – $EV 13,43
• Spieler 4: 3800 – $EV 25,00
• Spieler 5: 2700 – $EV 19,75 (Wir)

Spieler 3 geht nun mit seinen restlichen 1700 Chips All In und wir halten im Big Blind AQo, alle anderen Spieler haben gefoldet. Zunächst müssen wir Spieler 3 eine Range von Händen geben, mit der wir unsere Gewinnwahrscheinlichkeit für den Showdown berechnen können. Danach betrachten wir die veränderten Erwartungswerte und bestimmen damit, ob wir callen oder folden sollten.

Im Laufe dieses SnG haben wir bemerkt, dass Spieler 3 ein relativ tighter Spieler ist. Aufgrund der gerade gestiegenen Blinds schätzen wir, dass seine möglichen Hände alle Paare, alle Ass Kombinationen und alle Broadway Hände enthalten kann. Mit dem Programm PokerStove oder dem PokerStrategy Equilator errechnen wir gegen diese Range mit AQo eine Gewinnwahrscheinlichkeit von 60,6%. Für den Showdown sind wir schon einmal Favorit – nun müssen wir aber noch die veränderten $EV betrachten, um herauszufinden welche der beiden Aktionen Fold oder Call den höheren Erwartungswert besitzt.

Wenn wir folden bleibt unser $EV bei 19,75. Betrachten wir die Erwartungswerte für den Call wenn wir den Showdown gewinnen oder verlieren. Im Fall eines Gewinns scheidet Spieler 3 aus und wir besitzen 4400 Chips. Verlieren wir diesen Showdown, bleiben uns nur noch 1000 Chips und Spieler 3 kann auf 3400 verdoppeln. Im Falle des Gewinnes steigt unser $EV auf 29,0 – wenn wir verlieren sinkt er auf $EV 8,42. Berechnen wir nun diese Werte mit den Gewinnwahrscheinlichkeiten, können wir eine Aussage über den Erwartungswert des Calls machen und diese mit den anderen möglichen Aktion(Fold) vergleichen.

In 60,6% der Fälle werden wir über einen $EV von 29,0 und in den restlichen 39,4% über $EV von 8,42 verfügen. Die Rechnung sieht wie folgt aus:

$EV = (60,6% x 29,0) + (39,4% x 8,42) = 17,57 + 3,32 = 20,89

Im Durchschnitt steigt also der Erwartungswert von $EV 19,75 auf $EV 20,89 und wir sollten callen. Würden wir in dieser Situation 66 halten, würden wir gegen die Range von Spieler 3 zwar immer noch eine 53,6% Gewinnwahrscheinlichkeit haben, unser $EV würde insgesamt aber leicht fallen weswegen ein die richtige Aktion der Fold wäre. Wir können euch nur empfehlen, eines der ICM Poker Tools zu benutzen und verschiedene Situationen einmal durchzuspielen. Ihr werdet schnell bemerken, wie stark die unterschiedlichen Stacks eure gesamte ICM Poker Strategie beeinflussen.

Fazit

Richtet ihr in Turnieren alle eure All-In Entscheidungen nach dem Konzept des ICM, so spielt ihr mathematisch korrekter und macht automatisch auf lange Sicht einen höheren Profit. Bei der Anwendung des Independent Chip Model während des Spiels gibt es aber zwei Probleme: erstens ist die relativ komplizierte Berechnung am Pokertisch kaum durchzuführen, zweitens steht und fällt die gesamte Berechnung mit der korrekten Einschätzung der gegnerischen Hand Ranges.

Für die möglichst korrekte Anwendung des Independent Chip Model ist also viel Erfahrung notwendig. Ihr müsst einerseits lernen eure Gegner genau zu beobachten und deren Ranges für die unterschiedlichen Situation möglichst genau einzuschätzen. Gleichzeitig könnt ihr mit euren Hand Histories in einem ICM Poker Trainer diese Situationen nachstellen und analysieren. Ihr könnt diese Situationen auch verändern und so sehen, wie sich der Erwartungswert bei veränderten Chip Stacks oder Hand Ranges verändert. Mit der Zeit erhaltet ihr so ohne genaue Berechnungen ein immer besseres Gefühl dafür, ob ein Move profitabel ist oder nicht.